执教：张颖

教学内容：P27-28页例1和随后“练一练”，练习五1-3题。

教学目标：1.使学生经历解决问题的过程，初步体验选择合适的策略分析数量关系，确定解题思路的过程，形成相应的策略意识。

2. 使学生在选择策略解题问题的过程中，进一步积累分析数量关系的经验，体会画图、转化等策略在解决问题过程中的实用价值，增强运用策略解决问题的自觉性，提高分析和解决问题的能力。
3. 在参与数学活动的过程中，获得一些学习成功的愉悦体验，逐步形成乐于和同伴合作的积极情感，增强学好数学的信心。

教学重点：选择不同的策略解决与分数相关的实际问题。

教学难点：根据具体的情况选择合适的策略。

教学过程：

课前谈话：

有这样一个故事：

星期六的早晨，一位工程师打算在静下心来设计一份重要的图纸，他的妻子出去买东西了。但他的儿子小明却吵着闹着让工程师带他到游乐园去玩。

工程师在烦恼中从书架上拿出一本旧杂志，翻到一幅色彩鲜艳的大图画——一幅世界地图。

他三下五除二把这幅地图给撕了，撕成了十几块，对小明说：“如果你能把这幅地图给拼起来我就带你去游乐场。”

他心想：一个6岁的孩子没个半天时间是无法完成这个任务的，这样我就可以安安心心的设计图纸了……

但是不到十分钟后，工程师就听到敲门声，打开书房门，他的儿子小明把那幅拼好的地图递给了他。他十分震惊，就是自己也不可能在这么短的时间完成这个任务。小明是怎么做到的呢？

如果是你，你能这么快的拼好世界地图吗？

小明看到爸爸非常惊讶，很自豪的把图翻了过来，将图的背面展示给他爸爸看。工程师看了背面恍然大悟，直夸小明聪明，决定遵守自己的诺言，带小明去游乐园玩。

图的背面是什么呢？ （一幅汽车图片）

故事讲完了，你有什么想说的呢？（善于观察，肯动脑筋）

一、旧知链接  

师：过去我们已经接触过不少的策略，让我们翻开以前的课本，一起来回顾一下——

（课件）画图、列表、一一列举、转化……

那我们能不能根据问题的特点和解决问题的需要，灵活地选用这些策略解决问题呢?这节课我们继续来关注策略。进一步学习根据实际问题选择合适的策略解决问题。(板书课题)

二、新知探究

1、学习例1    

今天这节课我们将在原来的基础上，继续运用转化的策略解决一些有关分数与比的实际问题。

出示例1

1. 独立思考     

请一人读题，同学们想一想；这道题我们可以怎样解决呢？          

（2）小组讨论     

先不急着说出来，我们先在小组里交流，看哪一小组的方法多。

（师巡视找出不同的方法，留作稍后集体交流）

（3）集体交流           

哪一小组愿意和大家交流一下你们的想法？

 

（4）小结                 

听了她的讲解，大家还有什么问题要问她吗？

（如果学生没有，则我还有两个疑问，可以问问她吗？）

　　Ａ、你为什么要进行这种转化呢？

师：将一个复杂的问题转化成了一个简单的问题。

                                        （板书：复杂   简单）

　　Ｂ、你是怎么转化的？联系了什么知识？

师：同样的一个问题，同学们想出了不同的办法。把没有学过的知识转化成我们已经学过的知识就好解决了！

（5）独立完成

接下来就请同学们从这多样的方法中选择一种把它写下来，好吗？

 

 

2、试一试           

看看这两道题，你会不会呢？口说无凭，下面还是请大家自己先在作业纸上试试看。

（1）一套课桌椅的价钱是144元，其中椅子的价钱是课桌的 ，椅子的价钱是多少元？

（2）赵大娘家养的公鸡与母鸡只数的比是4:7，公鸡比母鸡少30只，赵大娘家养的公鸡有多少只？

 

三、丰富体验            

咱们接着看——

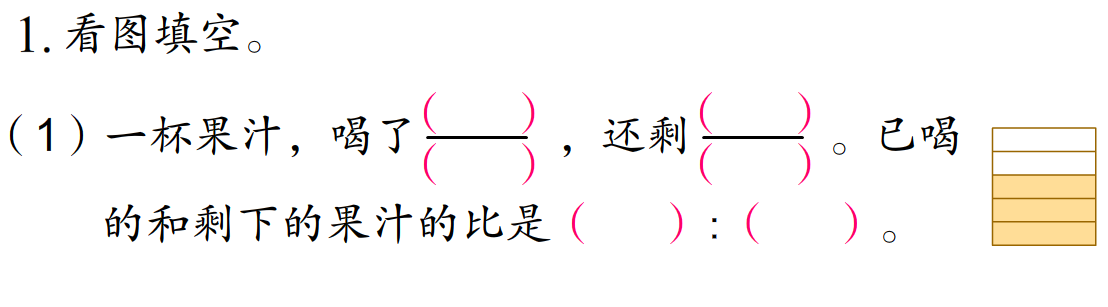
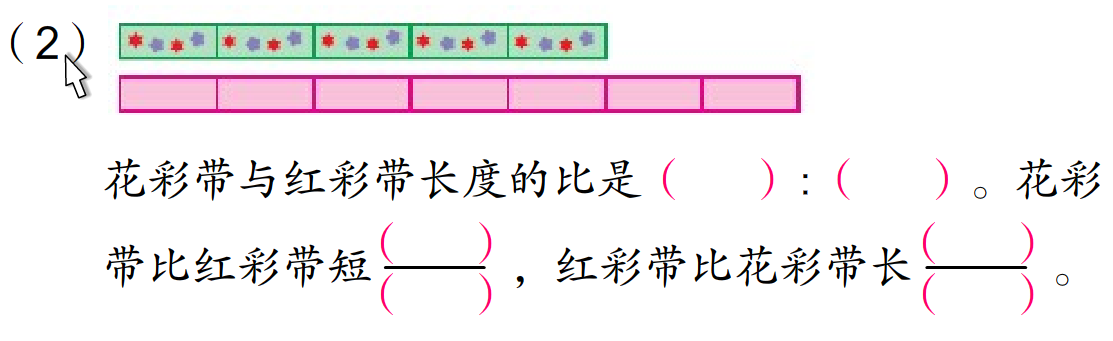
（1）你会做吗？指名口答。

（3）谁来说说你是怎样想的？

 

师：这儿还有几道题，也先请大家在自己的作业纸上试一试，好吗？

　　　　　　　     

（1）独立完成。

（2）学生的算法介绍和教师的评介。

　　　

四、自觉应用    

这儿还有一个有趣的问题，我们一起来想一想。

苏步青是我国著名的数学家，曾有人给他出过这样一道题

：甲、乙两人同时从距离是50千米的两地出发，相向而行。甲每小时走3千米，乙每小时走2千米，甲带着一只小狗，狗每小时跑5千米。这只狗同时和甲一起出发，当它碰到乙后，便回头跑向甲；碰到甲后又掉头跑向乙……如此下去，直到两人相遇。小狗一共跑了多少千米？

（1）先请大家自由地把题目读一读。

谁能说说这个题目什么意思？还请大家先自己试一试。

（2）大部分同学还在思考，这样谁先来告诉大家，你觉得这道题什么地方让你觉得不太好解决？

知道题目难在哪儿是一种水平！

（小狗不停地往返，每段所走的路程不好求。）

师：我第一次看到这道题时也是这样想的。

（3）XXX同学是这样做的，我们听听他是怎样想的，同时思考一下：他哪里和我们想的角度不一样？

（4）XXX同学讲自己的解法。

师：讲得真好！苏步青爷爷当时也是这样想的，我们把最热烈的掌声送给他！

（5）师：他哪儿和你想得不一样？

（学生阐述，教师相机点拨：

分段思考到整体思考，抓变化的路程转变为抓不变的时间）

（6）回顾他的这个解题过程其实不就是一个不断转化的过程吗？课件：

小狗一共跑了多少千米？转化为小狗一共跑了多少时间？转化为甲乙各走了多少小时？

其实我们解决很多数学问题的过程不都是这样不断转化的吗？

你们的表现太棒了！

 

五、反思提升         

（一）学生谈收获

师：好了孩子们，不知不觉中一节课就快过去了，大家觉得时间过得快吗？学得开心吗？有收获吗？

（二）教师作小结

师：转化是我们解决数学问题中很重要，很常用的一种策略。匈牙利著名数学家　　路莎�彼得说过这样的话——

  “数学家往往不是对问题进行正面的攻击，而是不断地将它变形，直至把它转化为已经得到解决的问题。”

　　　　匈牙利著名数学家　　路莎�彼得（Ross Peter）

这不正是我们刚才所体味到的吗？好了同学们，这节课我们就上到这儿，下课！

 

板书：

选择合适的策略解决问题

                      

        

      原问题                                          新问题

                   

复杂                                              简单

未知                                              已知